
All students hear the same script ending with, “and if there are no more questions, you may begin.” The proctor writes down start and stop times, then sits down. Everyone opens their testing books, takes out their freshly-sharpened pencils, and begins several grueling hours of testing.
For many educators, when they hear “summative assessment,” this is what they imagine. This stereotype is especially pronounced in math, where students worldwide are routinely tested and many questions have unequivocally correct numerical answers. There is some truth to this stereotype, too. Anyone who has taken the SAT or a timed state assessment might feel their palms sweat when reading the opening paragraph.
However, summative assessment can also be a force for good. This tool allows teachers to measure learning and assign grades at a classroom level. It can also measure the overall performance of a district, state, or even country when assigned rigorously and judiciously. In this article, I examine different types of and perspectives on summative assessment, describing what it means along with some of its benefits and pitfalls.
What is a summative assessment in mathematics?
Summative assessment is one type of assessment that occurs after learning is complete and is an evaluation of a test taker’s knowledge, skills, and abilities. A summative assessment can fit into a classroom or school in many ways, such as a unit test to assess learning at the end of unit, a final exam to assess learning at the end of a course, or statewide tests, which measure how well students have achieved state-level math standards. Students may also take national- or international-level summative assessments, such as the SAT, which use their own sets of standards.
Note the duality of what “summative assessment” can refer to. In terms of how it appears in the classroom, it broadly appears as either classroom summative assessment, like the example of a unit test, or as a standardized summative assessment, such as a statewide test. These types of assessments can look very different in practice, but overlap in terms of how they are both used to evaluate students after learning is complete.
Many summative assessments, especially the common examples of chapter quizzes and unit tests, are graded. Educators use summative assessment to gauge student mastery, not to determine what to teach next. That is, “summative assessment is commonly used to measure learning and is rarely used for learning” (Ismail et al., 2022). A summative assessment should help educators, policymakers, and other stakeholders understand students’ proficiency against a predefined set of criteria, such as state standards. It should also help students properly gauge their performance in a class and articulate what they know and can do.

Summative assessments in math often look like multiple-choice, matching, and fill-in-the-blank questions, such as these examples found in Into Algebra 1.
The difference between diagnostic, formative, and summative math assessments
There isn’t total agreement in the literature on how to classify assessment and just what each classification means. A common way to break down assessment types—and a categorization that we often use across our blog—is into diagnostic, formative, and summative assessment. Here is how these categories differ from the teacher’s perspective.
- Diagnostic Assessment: An assessment is diagnostic when it comes before learning. It is used to “diagnose” what the student knows and can do and where they may need support.
- Formative Assessment: An assessment is formative when it comes during learning. It is used to guide instruction and help teachers know what to do next.
- Summative Assessment: An assessment is summative when it comes after learning has occurred. It is used to summarize what the student has learned.
Students benefit from diagnostic and formative assessments, too. These assessments help students recognize their own strengths and areas of improvement. Summative assessment results, however, are more useful to teachers.
There are other labels for assessment, such as interim, benchmark, and progress monitoring, but they can always be categorized under or between the three broad types laid out here. For more information on what distinguishes these three forms of assessment, see our article on the three different types of assessment. In another article, we drill down specifically into the theory and practice of math diagnostic assessment.
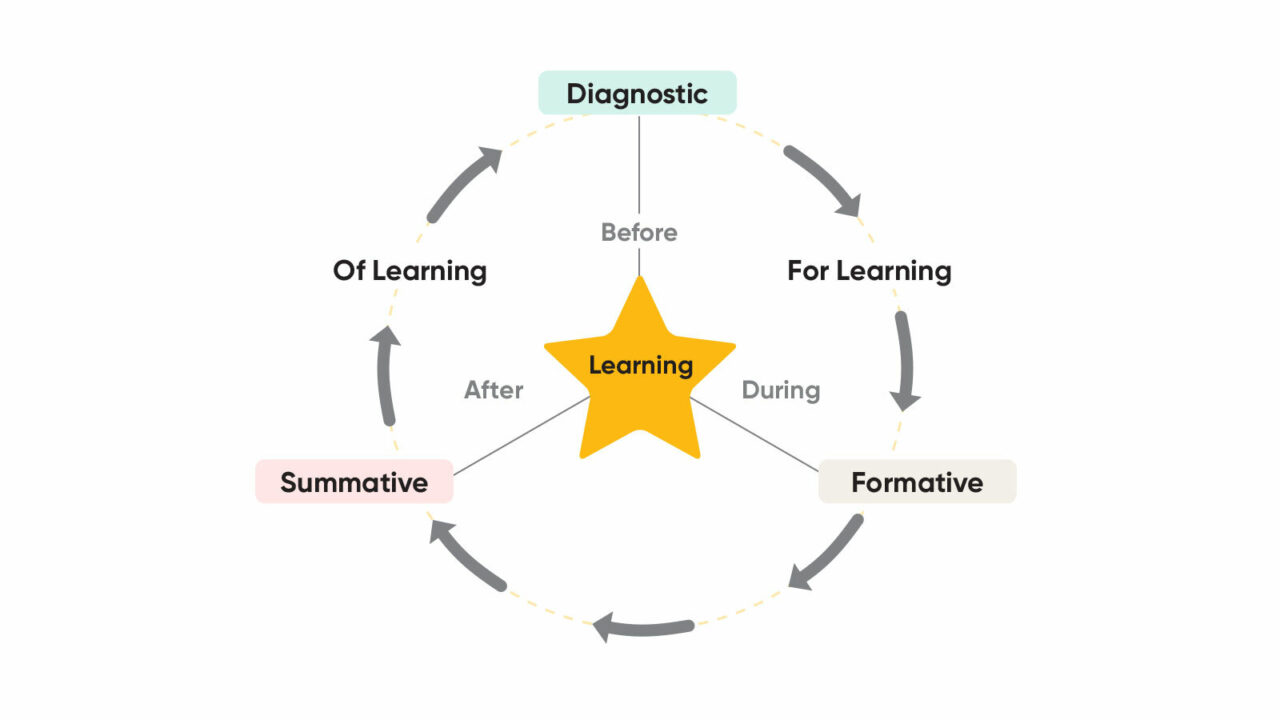
Assessment can be thought of as being broken into diagnostic assessment, which occurs before learning; formative assessment, which occurs during learning; and summative assessment, which comes after learning has occurred. Image is from The 3 Different Types of Assessment in Education.
Comparing formative and summative assessment
It is especially revealing to examine the differences between formative and summative assessment. At face value, these two types of assessment differ in timing and purpose, with summative assessment carrying higher stakes. These differences are elaborated in greater detail in our article on the purpose of summative assessment. Yet assessments can easily fall into a gray area where they are used with both formative and summative purposes.
In fact, formative and summative assessment are sometimes considered opposite ends of a spectrum. On one end, formative assessment is a quick, low-stakes assessment that occurs while students are still learning. On the other end, summative assessment is a time-consuming, graded, formal evaluation of student learning. According to Robert M. Capraro and M. Sencer Corlu (2013), “almost any assessment can be used in a formative or summative way.”
Chytrý and Kubiatko (2021) describe summative assessment as given to students “at the moment when they can no longer change their results.” Formative assessments are instead used to help teachers adapt their instruction and improve students’ understanding of the concepts or standards before they’re tested on mastery. In general, formative assessment uses student data to inform teaching whereas summative assessment uses student data to evaluate learning outcomes (AERA, APA, & NCME, 2014).
Formative assessment doesn’t carry the same stakes or induce the same anxiety as summative assessment. However, summative assessment tells us information that formative assessment cannot. At the most extreme scale, only through large-scale summative tests, for example, do we know that mathematics achievement has been on average increasing in the U.S. since the 70s, with a noticeable drop during the pandemic (National Center for Education Statistics, 2022).
What’s special about math?
Much of this article could apply just as well to any subject. However, when it comes to assessment, mathematics is in some ways unique. In the seminal book Visible Learning for Mathematics, Grades K–12, John Hattie et al. explain that a “fundamental part of understanding mathematics is to realize how concepts grow and expand over time” (2016, p. 209).
Math builds on itself in a way that is different from any other subject. Consider a student who excels in multiplication but struggles with fractions. At some point, the student will need to learn how to multiply fractions. Concepts envelop one another neatly in this way. Counting leads to addition, which in turn leads to multiplication and exponentiation. Points lead to lines, which in turn lead to planes and 3-D space. It is only within the past few decades that the importance of developing algebraic thinking in early elementary grades has been demonstrably linked to later success in formal algebra courses (Hodgen, Oldberg, & Strømskag, 2018).
Math is also unique in how it serves as a foundation for many STEM concepts. Mathematical literacy is a “gateway to technological literacy and to higher education” (Schoenfeld, 2002, p. 3). It is not enough to merely be able to add and multiply fluently; success in scientific courses requires at times reasoning and communicating clearly using the language and notation of mathematics. Math proficiency may not be required to engage in problems outside STEM fields, but it is always an advantage, with applications everywhere, including art, sports, fashion, and food, to name a few.
The benefits of summative assessment
There is a reason that summative assessment is inescapable. Understanding children’s math capabilities can be of great importance not just for their teachers and families, but for “policy-makers, curriculum-makers and for future employers” (Chytrý & Kubiatko, 2021). Schools want to know when to invest in specific math programs. Districts want to know which schools are performing strongest in math. Entire countries want to know how their children compare to other children globally. (According to the PISA 2022 results, the U.S. outperforms most countries, but lags behind several dozen. The highest-ranking country is Singapore.)
While teachers can and should evaluate, contextualize, and communicate students’ abilities to families and other stakeholders, one person can neither do that at a large scale nor fully get inside a student’s head. Thus, there is a need for a “device or procedure in which a sample of an examinee’s behavior [in math] is obtained and subsequently evaluated and scored using a standardized process” (AERA, APA, & NCME, 2014, p. 2). The practical problem of assigning students grades and being able to answer whether they are performing at grade level requires some amount of summative assessment.
Students benefit from being able to review their performance on summative assessments, as well. It is an opportunity for them to reflect critically on what skills and concepts they know so far. “Did you ever take a mathematics test and have to wait a week for it to be graded and returned?” pose researchers John Hattie et al. (2017, p. 211). “Students still deserve and should receive timely feedback on what they know or need to learn to be prepared for the next unit of study.”

Students, educators, and policymakers all need summative assessment to some extent, yet there are challenges that come with assessing student knowledge.
The challenges of summative assessment
Despite the need for summative assessment, there is no escaping some of the challenges that come with assessing student knowledge. For one, students are people. Many attributes can sully assessment results, such as test anxiety, social marginalization, or disabilities like dyscalculia. Math test items invariably assess the student’s linguistic background and prior knowledge, too (Cheuk, Daro, & Daro, 2018). Otherwise prepared students may falter simply for being multilingual learners.
These factors are addressed as best as possible when developing both standardized assessments and test-taking accommodations that are part of students’ Individual Education Programs (IEPs) or 504 plans. Yet, test scores will always depend to some extent on the environment and experiences of both the test-givers and test-takers. Stakeholders are sometimes unfairly held accountable for student test scores, an aspect of summative assessment that has “drawn widespread concern” (Zwick, 2022, p. 149).
An additional challenge is that students can get caught in a negative feedback loop. They perform poorly in tests, become discouraged and assume they’re not “math people,” and consequently fall further behind. For lower achieving students, high stakes summative tests are “only a mechanism of certification and exclusion rather than a motivation for learning” (Iannone & Jones, 2017).
When to use a summative math assessment
The time to administer a summative math assessment is at the end of an instructional period, such as the end of a unit, semester, course, or academic year. More incremental summative assessment is often used to show measurable growth and give specific feedback after a lesson or unit, though these assessments fall into the gray area between formative and summative assessment.
Paul Black and colleagues (2011) point out that “summative assessments that are integrated within the daily pedagogy of teachers are problematic.” Summative assessments of mathematical understanding should not be too frequent. The actual number of times that students should have a summative assessment, however, is hard to pin down. Determining what assessments are necessary depends on the purpose of the assessment, such as the need to determine student grades, fulfill grant requirements, evaluate programs, and analyze school- and district-level data (Kamenetz, 2014). Ultimately, the approach to summative math assessment will not be identical for two different schools and often not even for two teachers in the same school.
How to write an effective summative assessment in math
Research-based best practices around writing assessment items are outside the scope of this article. In part this is because it is a subjective practice that is both art and science. “Item writing lacks the rich theoretical tradition that we observe with statistical theories of test scores,” writes educational psychologist Thomas Haladyna (2004, p. 271). In addition, summative assessments typically come ready-made for teachers, either as part of the curriculum or through larger test development organizations.
For educators wanting to create their own assessments, it is of course possible, albeit demanding. Greg Conderman and Carol Koroghlanian spell out some broad principles in “Writing Test Questions Like a Pro” (2002), such as testing only one idea in a question, avoiding “all of the above” and “none of the above,” and restricting matching questions to ten items or less. These sorts of best practices have remained demonstrably valid for decades, yet they are only the tip of the iceberg. There is a staggering amount of work behind developing a test that is valid, reliable, and as bias-free as possible, which helps to explain why it is so time-consuming and expensive to develop and administer large-scale tests like the SAT.
As discussed throughout this article, math assessments vary widely. As long as the assessment is designed to understand how well students have mastered specific mathematical ideas or standards, the format can be a portfolio, presentation, or other type of project-based learning task. Robert Capraro and M. Sencer Corlu (2013) provide some guidelines for creating project-based learning tasks that can be summative assessments:
- Plan the summative project at the same time as when you develop lessons.
- Provide closely aligned formative feedback before having students complete the summative project.
- Provide students in advance with a rubric, and guide them in how to interpret it so that no part of the assessment comes as a surprise.
“Math lends itself to problem solving, the very nature of math,” writes educator Todd Stanley, arguing that project-based learning assessments are generally better for math teaching (2017). He cautions, however, the complexity of making “questions that challenge students to analyze, evaluate, and create.” Problems should be created in a way that gets at higher-level questioning, where students can apply their understanding of specific knowledge, skills, and abilities.

Into Math features unit projects that can be used to summatively assess student performance, such as this Unit 3 project that involves making and analyzing graphs.
Summative assessment examples in math
As explored throughout this article, assessment is summative so long it is used to measure math knowledge. It does not need to look like a typical standardized test. A summative math assessment can take a variety of forms:
- End-of-Unit Tests and End-of-Chapter Quizzes: Perhaps the most common form of summative assessment is the test that students take after completing a unit or chapter in a course. For the assessment to be purely summative, it should be graded, reflective of learning that’s been completed, and not designed to inform future instruction.
- Midterm and Final Exams: Major tests that cover half or all of a course’s content are more common for older students and represent an assessment of a large swath of learning. Final exams are a clear example of summative assessment, as they sometimes represent a large portion of a student’s grade and are taken at a time when there’s no time left for a teacher to use assessment results to inform subsequent teaching.
- Standardized State Assessments: The exact topics and assessed grade levels depend on the state, but almost all states test students annually using some form of large-scale math assessment to understand students’ proficiency at a school, district, and state level.
- Standardized Federal Assessments: Sometimes the goal is to understand students’ math performance at a countrywide level to check on nationwide progress and compare U.S. achievement to other countries. Math assessments from organizations like TIMSS, PISA, and NAEP are given every few years to select groups of students.
- Standardized Achievement Tests: These are typically aimed at measuring mathematical learning that has happened across years, if not one’s entire life so far. Tests like the SAT or ACT assess overall math understanding and problem-solving ability to predict success in college.
- Cumulative Projects: Students work towards a project that incorporates what the student is expected to have learned. This type of summative assessment can be more motivating than a typical test (Capraro & Corlu, 2013).
- Math Portfolios: A capstone portfolio can include written, visual, and orally presented parts as a way for students to show their math learning.
Attention should be given to the last two summative assessment examples: cumulative projects and math portfolios. For teachers, although these are usually more time-consuming to grade than a multiple-choice test, they get insights into how a student describes, writes about, and solves a problem—especially a broad one that addresses multiple standards and a range of concepts. Those insights can be part of assessing a student in math.
Students benefit, too. They are not subjected to a test that exists only at the moment and are instead evaluated on a more authentic work sample that they have time to develop. Math education researcher Rosemary Callingham (2010) explains that these are “affirming and powerful demonstrations to the child, and others, of what he or she has learned.” In the case of portfolios, when students sift through a yearlong body of work to look for the best possible evidence of achievement, “it changes their perspective about their learning and their work” (Picone-Zocchia & Martin-Kniep, 2008).
Summing it up
Fortunately, you are not required to complete a formal assessment of this blog’s content.
I kid, but there’s no question that summative assessment is inextricably tied to teaching mathematics and is used by educators, policymakers, and even the test-takers themselves to understand how well students understand math.
Summative assessment is inevitable, and it is balanced with other forms of assessment that collectively measure student learning. Without a doubt, summative assessment in math can be effective and useful, but it is ultimately up to the teachers and school community to ensure that students are set up for success in math.
After all, no single summative assessment can fully capture student learning. Both making the test and taking the test are hard and fraught with the complexities inherent to being human.
***
Gain a complete picture of student achievement and drive student growth using HMH’s suite of assessment tools.
References
American Educational Research Association (AERA), American Psychological Association (APA), & National Council on Measurement in Education (NCME). (2014). Standards for Educational and Psychological Testing. American Educational Research Association. https://www.apa.org/science/programs/testing/standards
Black, P., Harrison, C., Hodgen, J., Marshall, B., & Serret, N. (2011). Can teachers’ summative assessments produce dependable results and also enhance classroom learning? Assessment in Education: Principles, Policy & Practice, 18(4), 451–469.
Callingham, R. (2010, August 16). Mathematics assessment in primary classrooms: Making it count. Research Conference 2010. Teaching Mathematics? Make it count: What research tells us about effective mathematics teaching and learning, Melbourne, Australia.
Capraro, R. M., & Corlu, M. S. (2013). Changing Views on Assessment for STEM Project-Based Learning. In STEM Project-Based Learning: An Integrated Science, Technology, Engineering, and Mathematics (STEM) Approach (2nd edition, pp. 109–118). SensePublishers. https://brill.com/display/book/9789462091436/BP000013.xml
Cheuk, T., Daro, P., & Daro, V. (2018). The Language of Mathematics and Summative Assessment. In A. L. Bailey, C. A. Maher, & L. C. Wilkinson (Eds.), Language, Literacy, and Learning in the STEM Disciplines (1st ed., pp. 187–205). Routledge.
Chytrý, V., & Kubiatko, M. (2021). Pupils’ Summative Assessments in Mathematics as Dependent on Selected Factors. Eurasia Journal of Mathematics, Science and Technology Education, 17(8). http://dx.doi.org/10.29333/ejmste/11112
Conderman, G., & Koroghlanian, C. (2002). Writing Test Questions Like a Pro. Intervention in School and Clinic, 38(2), 83–87.
Haladyna, T. M. (2004). Developing and Validating Multiple-Choice Test Items (3rd edition). Lawrence Erlbaum Associates.
Hattie, J., Fisher, D., & Frey, N. (2017). Visible Learning for Mathematics: What Works Best to Optimize Student Learning. Corwin. https://us.corwin.com/books/visible-learning-for-mathematics-255006
Hodgen, J., Oldenburg, R., & Strømskag, H. (2018). Algebraic thinking. In T. Dreyfus, M. Artigue, D. Potari, S. Prediger, & K. Ruthven (Eds.), Developing Research in Mathematics Education: Twenty years of communication, cooperation and collaboration in Europe (1st ed., pp. 32–45). Routledge. https://ntnuopen.ntnu.no/ntnu-xmlui/handle/11250/2497060
Iannone, P., & Jones, I. (2017). Special issue on summative assessment. Research in Mathematics Education, 19(2), 103–107. https://doi.org/10.1080/14794802.2017.1334578
Ismail, S. M., Rahul, D. R., Patra, I., & Rezvani, E. (2022). Formative vs. summative assessment: Impacts on academic motivation, attitude toward learning, test anxiety, and self-regulation skill. Language Testing in Asia, 12(1), 40. https://link.springer.com/article/10.1186/s40468-022-00191-4
Kamenetz, A. (2014, November 17). Testing: How Much Is Too Much? NPR Ed. https://www.npr.org/sections/ed/2014/11/17/362339421/testing-how-much-is-too-much
National Center for Education Statistics. (2022). NAEP Long-Term Trend Assessment Results: Reading and Mathematics. The Nation’s Report Card. https://www.nationsreportcard.gov/highlights/ltt/2022/
Picone-Zocchia, J., & Martin-Kniep, G. O. (2008). Supporting Mathematical Learning: Effective Instruction, Assessment, and Student Activities. Jossey-Bass.
Schoenfeld, A. H. (2002). Making Mathematics Work for All Children: Issues of Standards, Testing, and Equity. Educational Researcher, 31(1), 13–25. https://doi.org/10.3102/0013189X031001013
Stanley, T. (2017). 10 Performance-Based Projects for the Math Classroom. Prufrock Press Inc.
Zwick, R. (2022). A Century of Testing Controversies. In B. E. Clauser & M. B. Bunch (Eds.), The History of Educational Measurement: Key Advancements in Theory, Policy, and Practice (pp. 136–154). Routledge.
Get a free guide to choosing the right assessments for your district.












